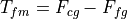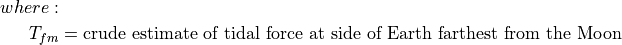Force Due to Gravity¶
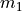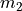The force due to gravity between two objects m_1 and m_2 is defined by the following equation.
F_{12} = \frac{-G\ m_1\ m_2}{r^2}
where:\\ F_{12} &= \mbox{gravitational force between }m_1\mbox{ and }m_2 \\ m_1 &= \mbox{mass of object 1} \\ m_2 &= \mbox{mass of object 2} \\ G &= \mbox{gravitational constant }(6.673*10^{-11}m^3kg^{-1}s^{-2}) \\ r &= \mbox{distance between the centers of }m_1\mbox{ and }m_2
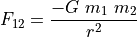
Tidal Forces¶
The tidal force is the change of gravity with distance. For the math minded you can differentiate the equation of force due to gravity, or make a very crude approximation of the tidal force on the surface of the Earth due to the Moon by very simple differencing of the gravitational force at the center of the Earth and the surface.
F_{cg} = \frac{-G\ M}{r^2}
where:\\ F_{cg} &= \mbox{gravitational force due to the Moon at the center of the Earth}\\ M &= \mbox{mass of the Moon} \\ G &= \mbox{gravitational constant }(6.673*10^{-11}m^{3}kg^{-1}s^{-2}) \\ r &= \mbox{distance between the centers of the Earth and Moon}\\
F_{ng} = \frac{-G\ M}{\left (r - R_{earth}\right)^2}
where:\\ F_{ng} &= \mbox{gravitational force from the Moon to the surface of the Earth to nearest the Moon} \\ M &= \mbox{mass of the Moon} \\ G &= \mbox{gravitational constant }(6.673*10^{-11}m^{3}kg^{-1}s^{-2}) \\ r &= \mbox{distance between the centers of the Earth and Moon}\\ R_{earth} &= \mbox{radius of the Earth}\\
F_{fg} &= \frac{-G\ M}{\left (r + R_{earth}\right)^2}
where:\\ F_{fg} &= \mbox{gravitational force from the Moon to the surface of the Earth farthest from the Moon} \\ M &= \mbox{mass of the Moon} \\ G &= \mbox{gravitational constant }(6.673*10^{-11}m^{3}kg^{-1}s^{-2}) \\ r &= \mbox{distance between the centers of the Earth and Moon}\\ R_{earth} &= \mbox{radius of the Earth}\\
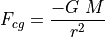
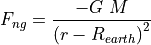
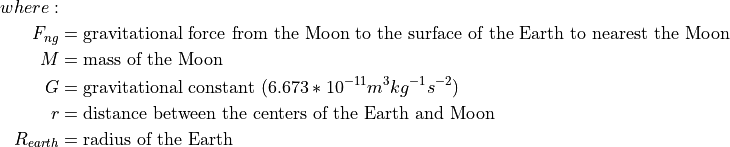
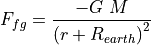
Double Bulge¶
Can use the equations from the previous section to explain the tidal bulge. There is a tidal bulge for every body near enough and big enough to the Earth. Water level measurements are only accurate enough to measure the tidal effect of the Moon and Sun. You can think of the Earth as turning underneath the tidal bulges from the Moon and Sun which causes the typically diurnal tidal cycle.
Why is there an outward bulge on the side of the Earth opposite of the Moon or Sun? This isn’t intuitive, but you can see that it is indicated in the equations above.
Tide as change in gravity on the nearest side of the Earth to the Moon and would be negative indicating a pull toward the Moon:
T_{nm} = F_{cg} - F_{ng}
where:\\ T_{nm} &= \mbox{crude estimate of tidal force at side of Earth nearest to the Moon}
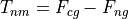
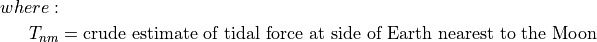
Tide as change in gravity on the farthest side of the Earth to the Moon and would be positive indicating a pull away from the Noon:
T_{fm} = F_{cg} - F_{fg}
where:\\ T_{fm} &= \mbox{crude estimate of tidal force at side of Earth farthest from the Moon}
